Confirmation bias. In the finance world, investors will often over-emphasize information that supports his existing thesis while actively ignoring information which might discredit that thesis. When looking for new information, that same investor only seeks additional information in places that might further support his existing thesis. He never even looks for information that might discredit it.
Ironically, many investors are well aware that this bias exists in general, but they deliberately ignore the fact that they themselves are exhibiting it. Confirmation bias squared.
In reality, after an attractive investment has already been identified, negative information is not only more useful to the investor, but it is also more practicable to evaluate. It leads to firmer conclusions which can actually be relied upon, as opposed to just interesting anecdotes.
Consider the logic test below. The relevance to investing should be immediately obvious.
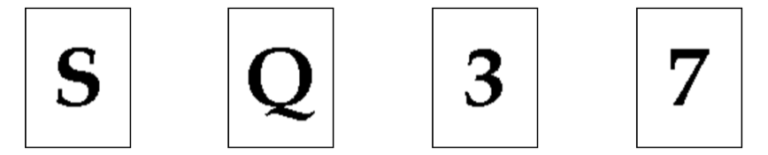
We have a deck of cards where every card has a letter on one side and a number on the other side.
Our goal is to test the thesis that: If a card has the letter S on one side then it must have the number 3 on the other side. (i.e. we are only testing for what happens next, once we see a letter S).
Question: Which two cards do we need to turn over to properly test that thesis above ?
Confirmation bias is more likely to occur in situations where there exists significant public disagreement. Rather than evaluating all information objectively, some investors lose site of the true, aggregate merits of their investment simply because they’ve become overly focused on a winning public debate. This is even more likely when the parties develop personal grudges against another. Their only goal becomes the ability to say “see, I told you so”, even when doing so may later result in financial losses to themselves.
The logic test above is known as the “Wason Selection Task”. The only cards we need to turn over are the S card and the 7 card. But many individuals tend to immediately turn over the 3 card, because that appears to be the easiest way to get immediate “confirmation” of their thesis.
If the 3 card happens to show an S on the other side, these people would then trumpet the fact that their thesis has seemingly been validated. They say “see, I told you so. Seeing S means we will find a 3”.
But in fact, regardless of what appears on the other side of the 3 card on this one particular instance, it tells us precisely nothing about the reliability of any longer pattern going forward.
Remember, we only care about proving what happens when we encounter an S. And our thesis is that when we do see an S, we will always find a 3 on the other side. Only by turning over the 7 card can we test this thesis. And there are only two possible conclusions that we can come to.
- If we turn over the 7 card and we see an S, then our thesis has been immediately invalidated.
Our thesis was proven wrong, because S would have led to 7.
- If we turn over the 7 card and we see anything other than an S, then we learn nothing.
Our thesis remains unconfirmed, neither right nor wrong.
As much as we would like to prove the thesis that S leads to 3, in many circumstances it is simply not possible to do so conclusively. But in the example above, there did exist some chance that we could conclusively disprove the S leads to 3. In the investment world, this ability to disprove would help prevent us from making some very expensive mistakes because we would not fall prey to unjustified over-certainty.
And yet many people will make the mistake of deliberately turning over the 3 card. Doing this would either show nothing or would actually mislead them into reliance on pattern that hasn’t actually been proven at all.
In a world where someone has infinite resources, one could simply turn over infinite cards and just keep track of all of the results. In that world, turning over the 3 card would be just fine. But in reality, we do not live in that infinity world, so it is important to conduct one’s research accordingly.
(Note: The Wason Test above was taken from PhilosophyExperiments.com).


